|
El método de Sorel consiste en un método analítico
donde se va calculando plato a plato resolviendo cada uno de los balances
de materia y energía para obtener los caudales de líquido
y vapor, la temperatura de plato y las composiciones.
Se suponen conocidas
o especificadas:
|
|
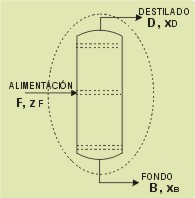
- Alimentación
(flujo, composición, presión y temperatura o entalpía):
F, zF, PF,
TF o hF
- Composición
de cabeza y fondo: xD , xB
- La presión de la columna
- La relación de reflujo: L1
/ D
- Características del condensador (total o parcial)
|
| La secuencia
de cálculo es la siguiente: |
|
1. Se realiza un
balance de materia global y por componentes
a la columna para obtener los caudales de destilado y de fondo.
|
 |
|
F
= D + B
|
|
|
| 2. Si
el condensador es total, la temperatura del destilado TD
será la de burbuja correspondiente a la composición xD.
De esta manera se determina la entalpía hD,L. |
| |
| 3. De
la relación de reflujo y el balance de materia se obtiene: |
|
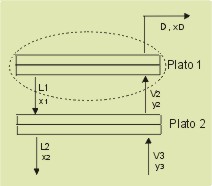
L1
= RR· D
|
 |
|
(siendo
RR la relación de reflujo)
|
|
|
| Como
la condensación es total se tiene que: |
|
y2
= x1 = xD
|
| 4. Ahora
se aplica el equilibrio al plato 2. Se considera
que el plato 2 es una etapa de equilibrio, por tanto su temperatura T2
será la de rocío de la corriente V2 y
la composición x2, la de la fase líquida
en equilibrio con y2. Con estos valores se determinan
las entalpías h2,V y h2,L. |
| 5. Se
realizan los siguientes balances
entálpicos: |
| a)
Para obtener el calor cedido en el condensador qD
se realiza el siguiente balance. |
|
V2·
h2,V + qD = (D+ L1)·
hD,L
|
| b) Para
conocer la temperatura del fondo TB,
hay que tener en cuenta que va a ser la de burbuja para la composición
xB. Con esto se calcula
la entalpía hB,L. |
| c) por
medio de un balance entálpico a la columna se deduce el calor aportado
en el hervidor: |
|
qB
= D· hD,L+ B· hB,L-
F· hF- qD
|
| 6.
A continuación se realiza un balance a la parte superior de la columna
para calcular la sección de rectificación. |
|
V3
= L2 + D
|
|
V3·
y3 = L2· x2
|
|
V3·
h3,V + qD = L2·
h2,L+ D· hD,L
|
|
h3,V
= h3,V (y3,T3)
|
| Se tienen
4 ecuaciones con 5 incógnitas: V3, y3,
h3,V, T3 y L2,
para resolverlo se precisa la condición de que T3
sea la temperatura de rocío correspondiente a la composición
y3. |
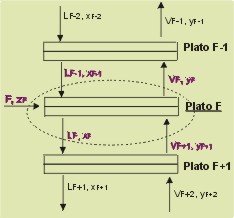
| 7. Para
realizar el cálculo de equilibrio al plato
3 se realiza de manera similar al paso 4, obteniendo x3
y h3,L |
| 8. Realizando sucesivos
balances a medida que se desciende por la columna se llega al plato
de alimentación. Se supone que se ha llegado a dicho plato
si xn <
zF. El balance a resolver es el siguiente: |
 |
|
F+
VF+1+ LF-1 = VF
+ VF
|
|
F·
zF+ VF+1· yF+1+
LF-1· xF-1 = VF·
yF + LF· xF
|
|
F·
hF+ VF+1· hF+1,V+
LF+1· hF-1,L = VF·
hF,V+ LF· hF,L
|
|
hF+1,V
= hF+1,V (yF+1,TF+1)
|
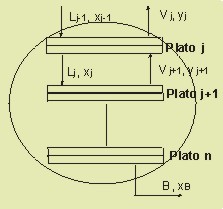
| 9. En la zona
de agotamiento se procede de igual manera, las ecuaciones son similares
salvo que ahora se hace el balance desde el fondo de la columna. Se habrá
alcanzado el último plato en el momento en que
xn <
xB. |
 |
|
Lj-1
= Vj+ B
|
|
Lj-1·xj-1
= Vj · yj + B·xB
|
|
Lj-1·hj-1,L
+ qB = Vj · hj,V
+ B·hB,L
|
|
hj,V
= hj,V(yj,Tj)
|
| |
|
Esta secuencia
de operación mostrada se puede realizar igualmente comenzando a
calcular los platos desde el fondo de la columna o bien empezando por
los extremos hasta llegar al plato de alimentación.
|



