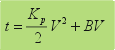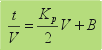| -
FILTRACIÓN
DISCONTINUA CON GRADIENTE DE PRESIÓN CONSTANTE |
| Esta
operación es frecuentemente utilizada en la industria. Su expresión
matemática se deduce a partir de la ecuación final obtenida
anteriormente: |
|
|
| Integrando
esta expresión se tiene |
 |
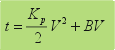y
de ahí |
 |
|
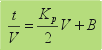| Para
calcular los parámetros Kp y B
se suele recurrir a la regresión lineal de los datos experimentales
obtenidos en laboratorio, de esta manera es posible conocer los valores
de la resistencia específica de la torta y la resistencia del medio
filtrante, Rm. |
| |
| -
LAVADO DE LA TORTA Y TIEMPO DE CICLO |
| Normalmente
las partículas sólidas separadas por filtración necesitan
ser lavadas para eliminar el filtrado atrapado entre los poros de la torta.
Se supone que la estructura de la torta no se afecta en el lavado y que
el caudal de lavado es el mismo que el de filtración. Para los filtros
en los que el lavado sigue el mismo recorrido que la filtración usando
el mismo gradiente de presión, el caudal de lavado es: |
|
|
| Sin
embargo en el caso del filtro prensa no ocurre lo mismo ya que el líquido
de lavado pasa a través de una torta el doble de gruesa que la filtrante,
por lo que el caudal de lavado resulta ser un cuarto del de filtrado. |
| Además
del tiempo de lavado se debe tener en cuenta que se precisa un tiempo adicional
para la separación de la torta y la limpieza. Por tanto el tiempo
total de ciclo es la suma de los tiempos de filtración, lavado,
limpieza y los tiempos muertos entre estas operaciones. |
| |
| -
FILTRACIÓN CONTINUA CON GRADIENTE DE PRESIÓN
CONSTANTE |
| En
estos filtros se considera que la resistencia del medio filtrante es despreciable
en comparación con la de la torta, esto quiere decir que B
= 0. Así si integramos la ecuación general de la filtración
se tiene que el tiempo requerido para la formación de la torta es: |
|
|
| Tomando
el tiempo de filtrado como una fracción del tiempo total de ciclo,
t = f· tc
y sustituyendo en la ecuación global se obtiene: |
|
|
| |
| -
FILTRACIÓN CON CAUDAL DE FILTRACIÓN
CONSTANTE |
| Este
tipo de filtración se da cuando se alimenta el filtro con una bomba
de desplazamiento positivo, así se tiene que: |
|
|
| Si
se parte de nuevo de la ecuación general y se despeja el gradiente
de presión: |
|
|
| Igual
que en el caso anterior, por regresión lineal se puede obtener el
valor de las constantes Kv
y C. |
| También
es posible expresar la ecuación anterior como una función
del tiempo sustituyendo el valor de V por la siguiente expresión: |
 |
|
| Se
observa que el gradiente de presión aumenta a medida que el espesor
de la torta crece y el volumen de filtrado aumenta. Sin embargo este incremento
de la presión afecta a las propiedades de la torta y a la velocidad
de producción de filtrado. La compresión actúa reduciendo
la porosidad, aumentando por tanto la concentración de sólidos
y como consecuencia va a variar la resistencia específica de la torta,
con lo que la respuesta producida será no lineal. |
| |
| -
TORTA COMPRESIBLE |
| Si
el análisis de los datos de filtración determina que se obtienen
distintas resistencias específicas y concentraciones de torta al
variar la presión, eso indica que la torta es compresible. En este
caso se suele utilizar una relación empírica para ajustar
los datos por regresión de la forma: |
| -
para la resistencia específica |
|
|
| -
o para la concentración volumétrica
de la torta |
|
|
siendo
constantes empíricas, donde n se denomina coeficiente de compresibilidad
que suele encontrarse tabulado. |
|
