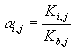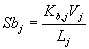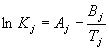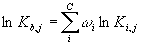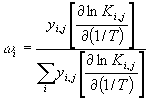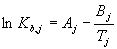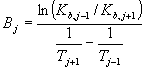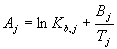Columna de destilación
Modelización
Para la simulación de las columnas de destilación vamos a usar el método Inside Out. Este
método no es un método matemático propiamente dicho como lo son los de
Newton y Runge-Kutta vistos anteriormente, sino más bien una forma de simplificar el
cálculo de un problema complejo, como es la resolución del sistema de ecuaciones no
lineales que constituyen el conjunto de equilibrios que se verifican en una columna de
destilación, facilitando y acelerando su solución.
Los métodos tradicionales están basados en dividir el sistema en varios bloques de forma
que se produzcan grupos de variables y ecuaciones que se resuelvan de manera
independiente. Lo más común es que estas variables de iteración sean algunas de las
variables primitivas del sistema, como la temperatura o la composición, y se agrupan con

aquellas ecuaciones en las que su efecto es más importante, es decir, los modelos
termodinámicos con la temperatura y los balances de masa y energía con las composiciones.
Estos sistemas de cálculo son poco generales y normalmente sólo sirven para casos más o
menos parecidos a aquel para el que se diseñaron.
Más generales son los sistemas basados en la aproximación de Newton-Raphson. En estos las
ecuaciones del sistema se linealizan mediante series de Taylor de primer orden utilizando
estimaciones de las variables primitivas. El sistema resultante se resuelve
iterativamente modificando las estimaciones hasta obtener una diferencia entre estimación
y valor obtenido lo suficientemente pequeña. Estos métodos presentan la ventaja de que
convergen rápidamente si las estimaciones iniciales son lo suficientemente buenas, pero
si no lo son la convergencia es muy difícil y resultan incluso peores que los anteriores.
El método Inside-Out se desarrolló para solventar algunos de los problemas típicos de los
anteriores y sus objetivos eran:
- Robustez en la solución incluso con pobres estimaciones iniciales.
- Generalidad en cuanto a su aplicación a todo tipo de destilaciones.
- Rapidez en la convergencia.
Como su nombre indica este método consiste en dos bucles anidados que se van a resolver
simultáneamente de forma iterativa, usando los resultados parciales de uno en la
resolución del otro. La gran ventaja que introduce es que en el lazo interno los modelos
termodinámicos rigurosos son sustituidos por unos modelos más sencillos que facilitan la
convergencia del bucle interno sin restar apenas precisión a los resultados. Con estos
modelos simplificados se resuelve el bucle interno obteniendo unos resultados parciales
de las variables de iteración internas que nos van a servir para, en el bucle externo,
calcular las variables termodinámicas de forma rigurosa y evaluar la bondad de nuestras
suposiciones, repitiendo el proceso hasta conseguir cerrar la iteración. Este método fue
desarrollado por vez primera por Boston y es el que implementan algunos de los más
conocidos simuladores químicos comerciales como Aspen-Plus o ChemCad.
Hay seis características fundamentales dentro del concepto Inside-Out:
- Los modelos complejos para el cálculo de K y de la entalpía se utilizan
únicamente para generar los parámetros de los modelos más sencillos. Los parámetros son
únicos para cada etapa en un sistema multietapa.
- Estos parámetros de los modelos simplificados se convierten en las variables de
iteración del bucle externo.
- Las variables de iteración del lazo externo son bastante independientes unas de
otras y de las variables primitivas por lo que una buena aproximación inicial no es tan
determinante.
- Las ecuaciones descriptivas del sistema se expresan en términos de los modelos
simplificados y están reordenadas de forma que se pueda obtener una solución completa para
las variables primitivas.
- Las variables de iteración internas combinan en cada etapa los efectos de la
temperatura y de la composición.
- Las variables primitivas resultantes de la resolución del bucle interno se usan
para calcular un nuevo juego de valores de las variables del bucle externo y en
caso de que la aproximación inicial hubiese sido correcta se habría conseguido la solución
del sistema.
Planteamiento del problema
Vamos a definir el problema del cálculo de una columna de destilación en régimen
estacionario. Suponemos las siguientes simplificaciones:
- Conseguimos el equilibrio de fases en cada plato.
- No se producen reacciones químicas en la columna.
- Las pérdidas de líquido en corrientes de vapor y viceversa son completamente
despreciables.

En un plato entra una corriente de alimentación mono o bifásica, con un caudal Fj, una composición
zi,j, y entalpía hFj esta corriente tiene una temperatura TFj y una
presión PFj que debe ser igual o mayor que la del plato j. Además entra una
corriente líquida proveniente del plato j-1, con un caudal Lj-1, composición
xi,j-1, entalpía hLj-1, temperatura Tj-1 y presión Pj-1 y una
corriente de vapor procedente de la etapa j+1 con las características: caudal
Vj+1, composición yi,j+1, entalpía hVj+1, temperatura Tj+1 y
presión Pj+1.
La etapa j es abandonada por dos corrientes en equilibrio, una líquida con las
propiedades Lj, xi,j, hLj, Tj y Pj, y otra de vapor
caracterizada por: Vj, yi,j, hVj, Tj y Pj. En nuestra
simulación no vamos a tener en cuenta posibles extracciones laterales ni calentamientos o
enfriamientos intermedios y en realidad vamos a contar con una única alimentación.
Asociadas a cada etapa teórica hay una serie de ecuaciones
comúnmente conocidas como MESH (masa, equilibrio, sumatorios y
entalpía) y que son:
- Balance de masa, una por componente y etapa:
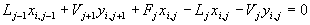
- Ecuación de equilibrio líquido vapor, una por componente y etapa:
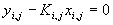
- Sumatorios, para líquido y vapor, uno de cada por etapa:
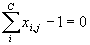
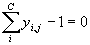
- Balance energético, una por etapa:
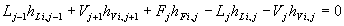
tenemos N(2C+3) incógnitas y si especificamos Fj, zi,j, TFj, PFj y
Pj, el modelo está también representado por N(2C+3) ecuaciones por lo que presenta una única solución.
Para la resolución del sistema mediante el método Inside-Out vamos a definir las
variables del bucle interno de la siguiente manera:
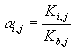
donde Kb,j es la constante de equilibrio de un componente hipotético b que tomamos como referencia.
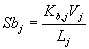
siendo Sb,j el factor de stripping para el coeficiente de referencia en la etapa j. En caso de contar con extracciones laterales distintas de las de cabeza y fondo deberíamos definir unas variables con información sobre su situación y sobre su magnitud, en nuestras columnas hemos prescindido de esta posibilidad.
Modelos simplificados
Generalmente, las constantes de equilibrio, K y las entalpías dependen de las
variables del sistema a través de unas relaciones representadas mediante complejos
modelos termodinámicos:
- K_i=K_i(T,P,x,y)
- H_L=H_L(T,P,x)
- H_V=H_V(T,P,y)
el calcular en cada iteración, cada componente y
cada etapa cada uno de estos valores supondría un volumen de cálculo que haría lentísima
la simulación, por ello una de las características más interesantes del modelo inside-out
es la utilización en el bucle interno de unos modelos simplificados para estas variables.
Estos modelos facilitan el cálculo de las temperaturas y las composiciones de cada etapa.
Para elegir un modelo simplificado para K debemos tener en cuenta su fuerte dependencia
de la temperatura, un modelo adecuado suele tener una forma semejante a:
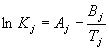
Para simplificar aún más el modelo vamos a definir un componente de referencia b cuya
Kcalcularemos, K_b como una media ponderada de la forma:
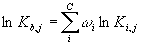
con
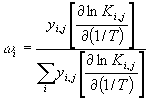
de esta manera el modelo final es:
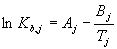
que se completa mediante la definición de un juego de volatilidades relativas a través de la expresión para a con las Kij obtenidas en el paso externo utilizando los modelos rigurosos. De esta forma para cada etapa se calcula un único valor de Kb y valores de aij. Para determinar los valores de Aj y Bj de la ecuación anterior debemos seleccionar dos temperaturas para cada etapa, por ejemplo la de la etapa anterior y la de la siguiente salvo en las etapas de los extremos, condensador y rehervidor, en que vamos a emplear la temperatura del plato adyacente y la de la propia etapa :
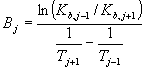
y
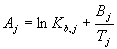
Para el cálculo de los modelos simplificados de la entalpía vamos a partir del valor de
la entalpía ideal de mezcla de la fase gaseosa hVº y vamos a calcular
discrepancias respecto a este valor para cada etapa, de modo que evaluaremos las
entalpías mediante la expresión:
La entalpía ideal de la fase gaseosa se calcula a partir de las entalpías ideales de cada componente mediante el modelo de mezcla ideal, y las discrepancias de entalpía se definen como:
- DhV=hV-hVº
- DhL=hL-hVº=lvap+DhV
y son las que se modelizan mediante funciones lineales simples que tienen la forma
- DHVj=cj-dj(T-T*)
- DHLj=ej-fj(T-T*)
con T* igual a la temperatura de referencia. Los parámetros c,d,e,f son evaluados a partir de los modelos rigurosos en cada paso por el bucle externo. En nuestro
caso no estimamos estos parámetros porque trabajamos en todo momento con el modelo para las entalpías.
Simulador
Última actualización 20/3/00
Por Pablo Díaz López
Correo electrónico:
pablo@diquima.upm.es