| En
primer lugar se debe conocer la resistencia global que se ofrece ante el
paso del líquido. Fundamentalmente el filtrado pasa a través
de dos resistencias en serie: |
| |
-
La resistencia total que se establece sobre el medio (incluyendo la
de las partículas incrustadas) que se llama resistencia
del medio filtrante y es importante durante los primeros momentos
de la filtración. |
| |
-
La resistencia que ofrecen los sólidos, y que no se debe al
medio filtrante, que se denomina resistencia
de la torta. La resistencia de la torta es cero al iniciar
la filtración, a causa de la deposición continua de
sólidos sobre el medio. Esta resistencia aumenta continuamente
con el tiempo de filtración.
|
|
| Hay
que tener en cuenta que en un filtro bien diseñado las resistencias
de las conexiones de entrada y salida son pequeñas y pueden despreciarse
en comparación con la resistencia de la torta y del medio filtrante. |
| |
| Por
tanto en la filtración por torta los factores más importantes
de los que depende la velocidad de filtración son: |
| |
-
la caída de presión desde la alimentación hasta
el lado más lejano del medio filtrante |
| |
-
el área de la superficie filtrante |
| |
-
la viscosidad del filtrado |
| |
-
la resistencia de la torta |
| |
-
la resistencia del medio filtrante y de las capas iniciales de la
torta |
|
| |
- CÁLCULO
DE FILTRACIÓN CONTINUA
|
| Para
calcular la resistencia a la filtración de
la torta, suponiendo ésta incompresible, se tiene la siguiente
expresión: |
|
|
se
observa que la resistencia de la torta depende de la porosidad y
la superficie específica  ,
respectivamente. ,
respectivamente.
|
|
| Y si
se desea se puede expresar como resistencia específica
(en m/kg): |
|
|
donde
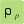 es
la densidad de la partícula. es
la densidad de la partícula. |
| El gradiente
de presión por unidad de altura de torta formada, L, se expresa a
través de la ecuación de Carman-Kozeny
: |
|
|
| siendo
U la velocidad superficial de
filtrado en un tiempo t: |
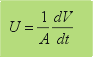 |
|
| y
donde V es el volumen de filtrado recogido
para un tiempo t. |
| A
medida que transcurre la filtración se van acumulando las partículas
que forman un determinado volumen de torta,
que se puede determinar por medio del parámetro: |
|
|
| Este
parámetro representa el volumen de torta formado en el paso de una
unidad de filtrado. |
| Sustiyendo
en la ecuación del gradiente se obtiene la siguiente expresión: |
|
|
| donde
quedan relacionados el volumen de filtrado, V,
con la altura de torta, L. |
| Otra
manera de establecer dicha relación se consigue con el siguiente
cociente: |
|
|
| donde
J es la fracción másica de sólidos
en la suspensión original. |
| Otro
parámetro muy empleado es la masa de torta seca por unidad de volumen
de filtrado: |
|
|
| donde
m es la masa de torta húmeda por unidad
de masa de sólidos secos contenidos en ella. |
| |
| Si
se incluye la resistencia del medio filtrante,
ésta se suele expresar como una altura de torta equivalente: |
|
|
| Este
volumen equivalente, Veq,
es el volumen de filtrado necesario para crear una altura de torta Leq
y depende únicamente de las propiedades de la suspensión y
del medio filtrante. |
| |
| Si
se combinan las dos resistencias señaladas se tiene una ecuación
general a partir de la cual se obtienen las ecuaciones de diseño
para los distintos tipos de filtración: |
|
|
| |
- CÁLCULO
DE FILTRACIÓN CENTRÍFUGA
|
| La
filtración
centrífuga es un caso especial de filtración donde
la fuerza de impulsión corresponde a la fuerza centrífuga.
|
| |
| Otros
tipos de filtración a considerar son: |
| -
filtración
discontinua con gradiente de presión constante |
| -
lavado
de la torta y tiempo de ciclo |
| -
filtración
continua con gradiente de presión constante |
| -
filtración
con caudal de filtración constante |
| -
torta
compresible |
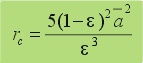
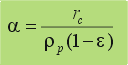
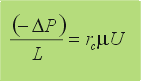
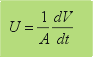
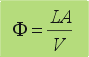
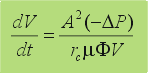
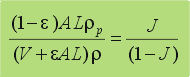
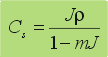
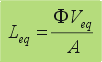
.gif)